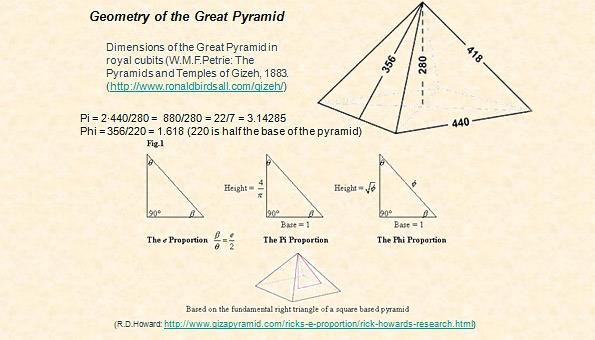
π: Η μυστηριώδης σταθερά
Κανένα άλλο μαθηματικό σύμβολο δεν προκάλεσε τόση απορία και τόσο ενδιαφέρον στην ανθρωπότητα και την επιστήμη, όσο η σταθερά «π». Σήμερα, στις 14/3, τέσσερεις χιλιάδες χρόνια μετά την «εμφάνισή» του, παραμένει ένα άλυτο μυστήριο.


 Αποκωδικοποιώντας την φύση
Αποκωδικοποιώντας την φύση 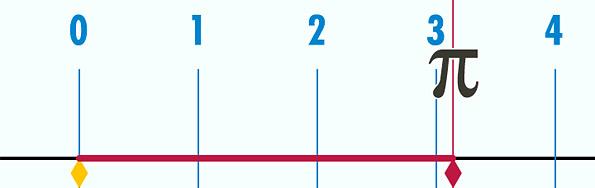
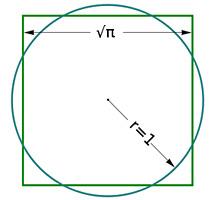 π
π